dp 数组的遍历方向

做动态规划问题时，肯定会对dp数组的遍历顺序有些头疼，拿二维dp数组来举例

有时候是正向遍历：

int[][] dp = new int[m][n];
for (int i = 0; i < m; i++)
    for (int j = 0; j < n; j++)
        // 计算 dp[i][j]

有时候反向遍历：

for (int i = m - 1; i >= 0; i--)
    for (int j = n - 1; j >= 0; j--)
        // 计算 dp[i][j]

有时候可能会斜向遍历：

// 斜着遍历数组
for (int l = 2; l <= n; l++) {
    for (int i = 0; i <= n - l; i++) {
        int j = l + i - 1;
        // 计算 dp[i][j]
    }
}

甚至更让人迷惑的是，有时候发现正向反向遍历都可以得到正确答案。

仔细观察的话，只要把住两点就行了：

1、遍历的过程中，所需的状态必须是已经计算出来的。

2、遍历的终点必须是存储结果的那个位置。

比如编辑距离这个经典的问题，我们通过对dp数组的定义，确定了 base case 是dp[..][0]和dp[0][..]，最终答案是dp[m][n]；而且我们通过状态转移方程知道dp[i][j]需要从dp[i-1][j],dp[i][j-1],dp[i-1][j-1]转移而来，如下图：

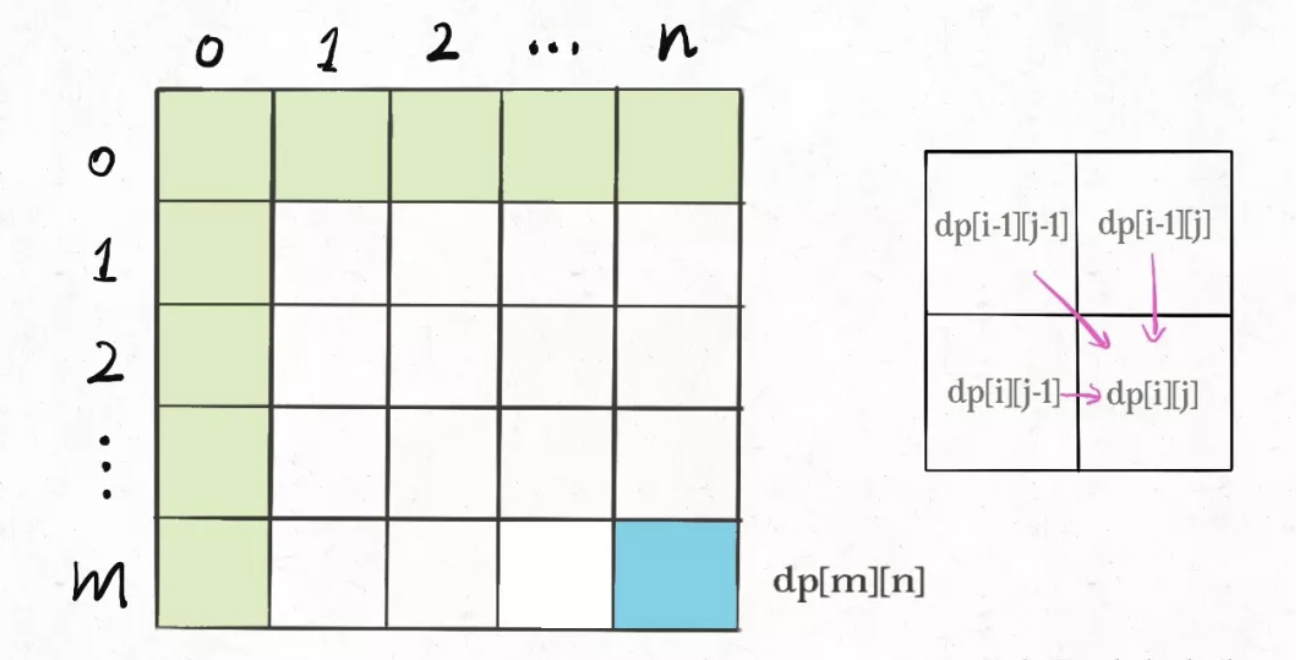
那么，参考刚才说的两条原则，该怎么遍历dp数组？肯定是正向遍历：

for (int i = 1; i < m; i++)
    for (int j = 1; j < n; j++)
        // 通过 dp[i-1][j], dp[i][j - 1], dp[i-1][j-1]
        // 计算 dp[i][j]

因为，这样每一步迭代的左边、上边、左上边的位置都是 base case 或者之前计算过的，而且最终结束在我们想要的答案dp[m][n]。