编辑距离

72.编辑距离

解决两个字符串的动态规划问题，一般都是用两个指针 i,j 分别指向两个字符串的最后，然后一步步往前走，缩小问题的规模。

1.递归

base case 是 i 走完 s1 或 j 走完 s2，可以直接返回另一个字符串剩下的长度。

对于每对字符 s1[i] 和 s2[j]，可以有四种操作：

if s1[i] == s2[j]:
    啥都别做（skip）
    i, j 同时向前移动
else:
    三选一：
        插入（insert）
        删除（delete）
        替换（replace）

⏬⏬⏬

public int minDistance(String word1, String word2) {
        return dp(word1, word2, word1.length() - 1, word2.length() - 1);
    }

    //返回 s1[0..i] 和 s2[0..j] 的最小编辑距离
    int dp(String s1, String s2, int i, int j) {
        // base case
        if (i == -1) return j + 1;
        if (j == -1) return i + 1;

        if (s1.charAt(i) == s2.charAt(j)) {
            // 本来就相等，不需要任何操作
            // s1[0..i] 和 s2[0..j] 的最小编辑距离等于
            // s1[0..i-1] 和 s2[0..j-1] 的最小编辑距离
            // 也就是说 dp(i, j) 等于 dp(i-1, j-1)
            return dp(s1, s2, i - 1, j - 1);  // 啥都不做
        } else {
            // 插入
            // 直接在 s1[i] 插入一个和 s2[j] 一样的字符
            // 那么 s2[j] 就被匹配了，前移 j，继续跟 i 对比
            // 操作数加一

            // 删除
            // 直接把 s[i] 这个字符删掉
            // 前移 i，继续跟 j 对比
            // 操作数加一

            // 替换
            // 直接把 s1[i] 替换成 s2[j]，这样它俩就匹配了
            // 同时前移 i，j 继续对比
            // 操作数加一
            return Math.min(
                    Math.min(dp(s1, s2, i, j - 1) + 1,    // 插入
                            dp(s1, s2, i - 1, j) + 1),    // 删除
                    dp(s1, s2, i - 1, j - 1) + 1 // 替换
            );
        }
    }

这段代码有点小问题就是，这个解法是暴力解法，存在重叠子问题，需要用动态规划技巧来优化。

对于子问题 dp(i-1, j-1)，如何通过原问题 dp(i, j) 得到呢？有不止一条路径，比如 dp(i, j) -> #1 和 dp(i, j) -> #2 -> #3。一旦发现一条重复路径，就说明存在巨量重复路径，也就是重叠子问题。

2.动态规划优化

常用就是用HashMap来做备忘录，避免重叠路径：

HashMap<String, Integer> map = new HashMap<>();

 public int minDistance(String word1, String word2) {
     return dp(word1, word2, word1.length() - 1, word2.length() - 1);
 }

 int dp(String s1, String s2, int i, int j) {
     if (map.containsKey(i + "*" + j)) {
         return map.get(i + "*" + j);
     }
     // base case
     if (i == -1) return j + 1;
     if (j == -1) return i + 1;

     if (s1.charAt(i) == s2.charAt(j)) {
         map.put(i + "*" + j, dp(s1, s2, i - 1, j - 1));  // 啥都不做
     } else {
         map.put(i + "*" + j, Math.min(
                 Math.min(dp(s1, s2, i, j - 1) + 1,    // 插入
                         dp(s1, s2, i - 1, j) + 1),    // 删除
                 dp(s1, s2, i - 1, j - 1) + 1 // 替换
         ));
     }
     return map.get(i + "*" + j);
 }

或是用dp数组：

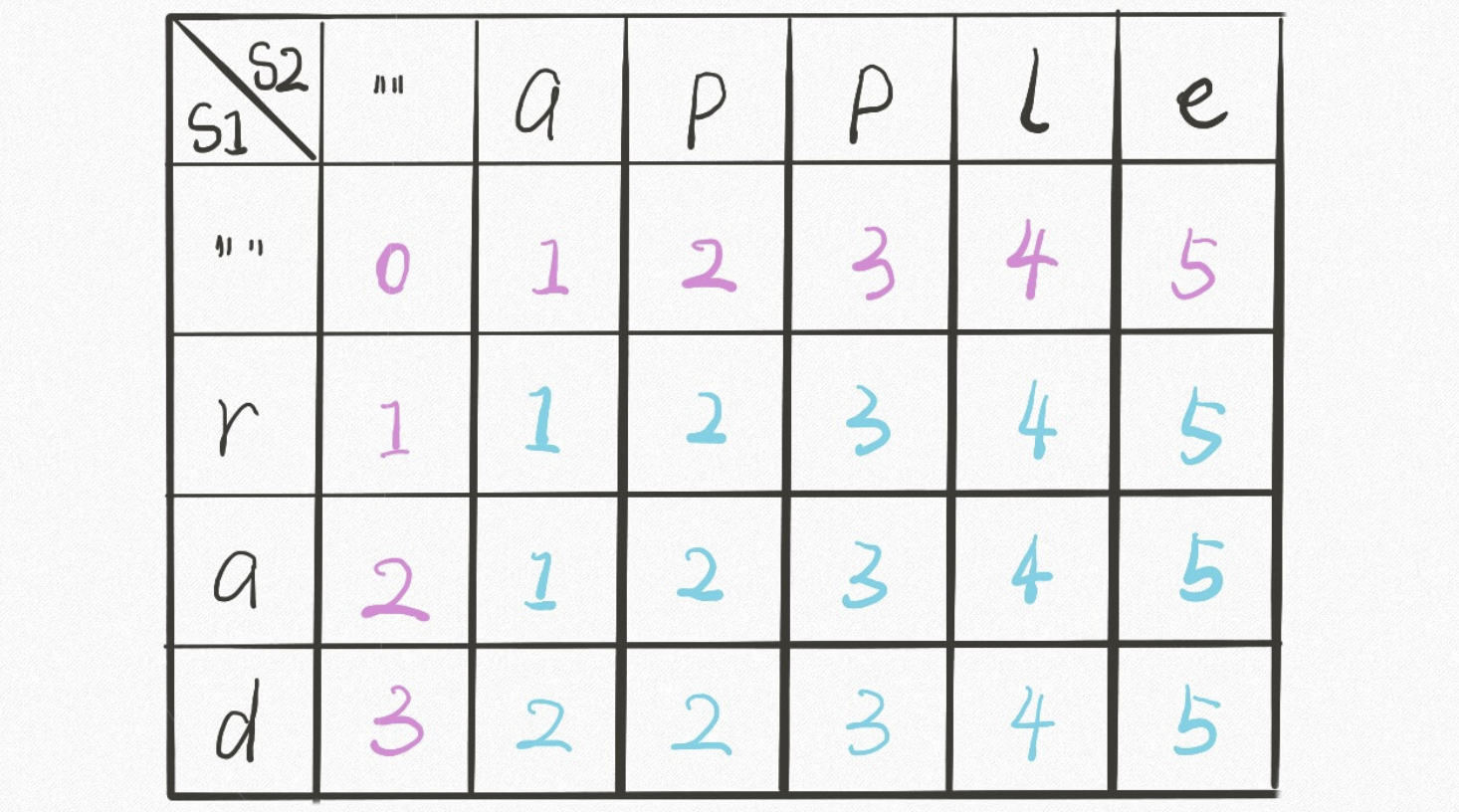
dp[..][0] 和 dp[0][..] 对应 base case，dp[i][j] 的含义和之前的 dp 函数类似：

int dp(i, j)
// 返回 s1[0..i] 和 s2[0..j] 的最小编辑距离

dp[i-1][j-1]
// 存储 s1[0..i] 和 s2[0..j] 的最小编辑距离

dp 函数的 base case 是 i,j 等于 -1，而数组索引至少是 0，所以 dp 数组会偏移一位。

既然 dp 数组和递归 dp 函数含义一样，也就可以直接套用之前的思路写代码，唯一不同的是，DP table 是自底向上求解，递归解法是自顶向下求解：

int minDistance(String s1, String s2) {
       int m = s1.length(), n = s2.length();
       int[][] dp = new int[m + 1][n + 1];
       // base case
       for (int i = 1; i <= m; i++)
           dp[i][0] = i;
       for (int j = 1; j <= n; j++)
           dp[0][j] = j;
       // 自底向上求解
       for (int i = 1; i <= m; i++)
           for (int j = 1; j <= n; j++)
               if (s1.charAt(i - 1) == s2.charAt(j - 1))
                   dp[i][j] = dp[i - 1][j - 1];
               else
                   dp[i][j] = Math.min(
                           Math.min(dp[i - 1][j] + 1,
                                   dp[i][j - 1] + 1),
                           dp[i - 1][j - 1] + 1
                   );
       // 储存着整个 s1 和 s2 的最小编辑距离
       return dp[m][n];
   }