最长公共子序列

1143.最长公共子序列

第一步，一定要明确 dp 数组的含义。对于两个字符串的动态规划问题，套路是通用的。

比如说对于字符串 s1 和 s2，一般来说都要构造一个这样的 DP table：

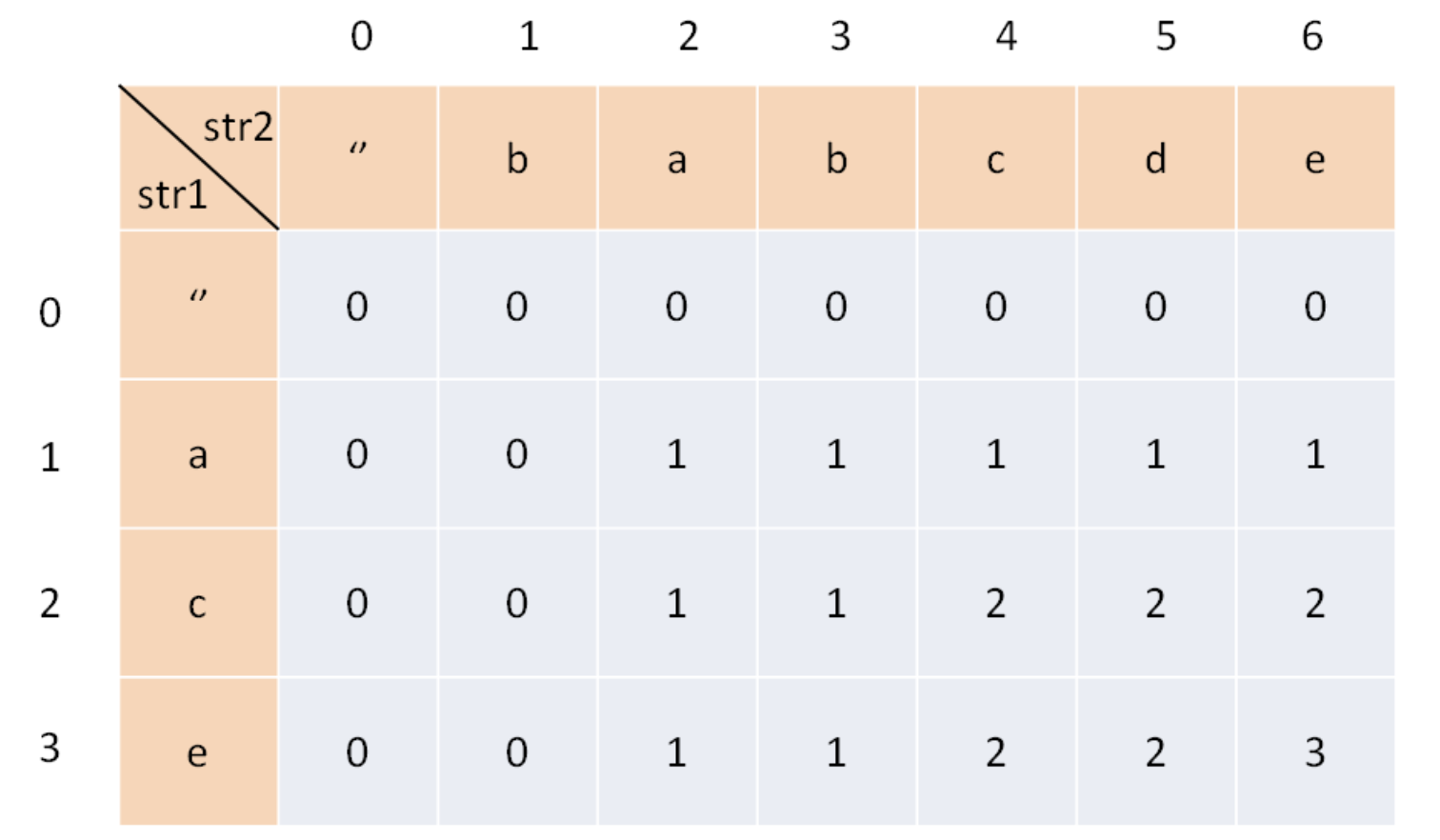
为了方便理解此表，暂时认为索引是从 1 开始的，待会的代码中只要稍作调整即可。其中，dp[i][j] 的含义是：对于 s1[1..i] 和 s2[1..j]，它们的 LCS 长度是 dp[i][j]。

比如上图的例子，d[2][4] 的含义就是：对于 "ac" 和 "babc"，它们的 LCS 长度是 2。最终想得到的答案应该是 dp[3][6]。

第二步，定义 base case。

让索引为 0 的行和列表示空串，dp[0][..] 和 dp[..][0] 都应该初始化为 0，这就是 base case。

比如说，按照刚才 dp 数组的定义，dp[0][3]=0 的含义是：对于字符串 "" 和 "bab"，其 LCS 的长度为 0。因为有一个字符串是空串，它们的最长公共子序列的长度显然应该是 0。

第三步，找状态转移方程。

这是动态规划最难的一步

状态转移说简单些就是做选择，比如说这个问题，是求 s1 和 s2 的最长公共子序列，不妨称这个子序列为 lcs。那么对于 s1 和 s2 中的每个字符，有什么选择？很简单，两种选择，要么在 lcs 中，要么不在。

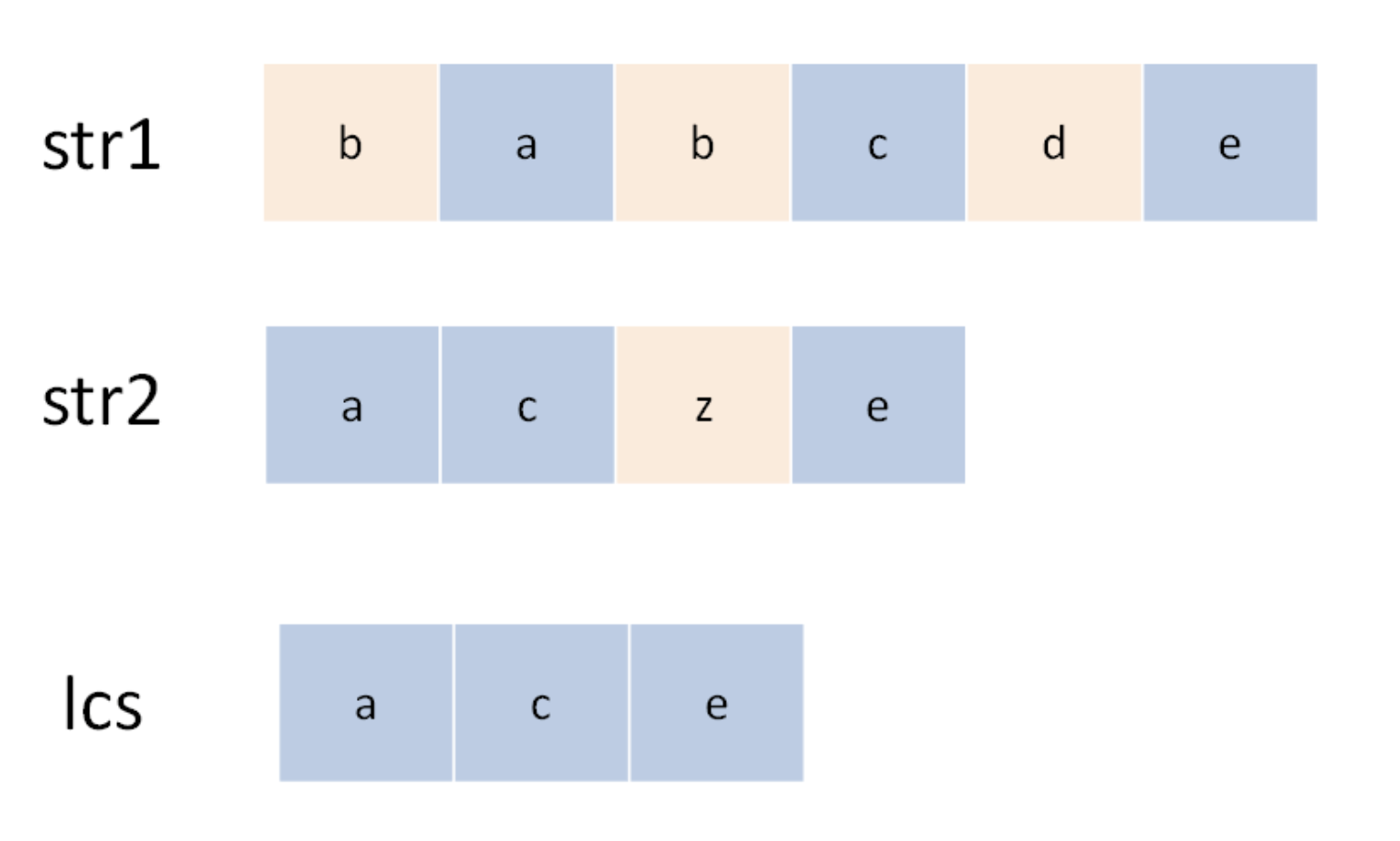
这个「在」和「不在」就是选择，关键是，应该如何选择呢？这个需要动点脑筋：如果某个字符应该在 lcs 中，那么这个字符肯定同时存在于 s1 和 s2 中，因为 lcs 是最长公共子序列嘛。所以本题的思路是这样：

用两个指针 i 和 j 从后往前遍历 s1 和 s2，如果 s1[i]==s2[j]，那么这个字符一定在 lcs 中；否则的话，s1[i] 和 s2[j] 这两个字符至少有一个不在 lcs 中，需要丢弃一个。先看一下递归解法，比较容易理解：

String str1;
  String str2;

  public int longestCommonSubsequence(String text1, String text2) {
      str1 = text1;
      str2 = text2;
      return dp(text1.length() - 1, text2.length() - 1);
  }

  int dp(int i, int j) {
      // 空串的 base case
      if (i == -1 || j == -1) {
          return 0;
      }
      if (str1.charAt(i) == str2.charAt(j)) {
          // 这边找到一个 lcs 的元素，继续往前找
          return dp(i - 1, j - 1) + 1;
      } else {
          // 谁能让 lcs 最长，就听谁的
          return Math.max(dp(i - 1, j), dp(i, j - 1));
      }
  }

对于第一种情况，找到一个 lcs 中的字符，同时将 i j 向前移动一位，并给 lcs 的长度加一；对于后者，则尝试两种情况，取更大的结果。

其实这段代码就是暴力解法，我们可以通过备忘录或者 DP table 来优化时间复杂度，比如通过 DP table 来解决：

int dp(String str1, String str2) {
      int m = str1.length();
      int n = str2.length();
      // 构建 DP table 和 base case
      int[][] dp = new int[m + 1][n + 1];
      //进行状态转移
      for (int i = 1; i < m + 1; i++) {
          for (int j = 1; j < n + 1; j++) {
              if (str1.charAt(i - 1) == str2.charAt(j - 1)) {
                  //找到一个 lcs 中的字符
                  dp[i][j] = 1 + dp[i - 1][j - 1];
              } else {
                  dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
              }

          }
      }
      return dp[m][n];
  }