四键键盘

发表于 | 分类于   |   次阅读
字数统计: 1,358 | 阅读时长 ≈ 6分钟

651.四键键盘

第一种思路

这种思路会很容易理解，但是效率并不高，直接走流程：对于动态规划问题，首先要明白有哪些「状态」，有哪些「选择」。

具体到这个问题，对于每次敲击按键，有哪些「选择」是很明显的：4 种，就是题目中提到的四个按键，分别是 A、C-A、C-C、C-V（Ctrl 简写为 C）。

接下来，思考一下对于这个问题有哪些「状态」？或者换句话说，需要知道什么信息，才能将原问题分解为规模更小的子问题？

第一个状态是剩余的按键次数，用 n 表示；

第二个状态是当前屏幕上字符 A 的数量，用 a_num 表示；

第三个状态是剪切板中字符 A 的数量，用 copy 表示。

如此定义「状态」，就可以知道 base case：当剩余次数 n 为 0 时，a_num 就是我们想要的答案。

结合刚才说的 4 种「选择」，可以把这几种选择通过状态转移表示出来：

1
2
3
4
5
6
7
8
9
10
11
12
dp(n - 1, a_num + 1, copy),    // A
解释：按下 A 键，屏幕上加一个字符
同时消耗 1 个操作数

dp(n - 1, a_num + copy, copy), // C-V
解释：按下 C-V 粘贴，剪切板中的字符加入屏幕
同时消耗 1 个操作数

dp(n - 2, a_num, a_num)        // C-A C-C
解释：全选和复制必然是联合使用的，
剪切板中 A 的数量变为屏幕上 A 的数量
同时消耗 2 个操作数

这样可以看到问题的规模 n 在不断减小，肯定可以到达 n = 0 的 base case，所以这个思路是正确的：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public int maxA(int N) {
       // 可以按 N 次按键，屏幕和剪切板里都还没有 A
       return dp(N, 0, 0);
   }

   // 对于 (n, a_num, copy) 这个状态，
   // 屏幕上能最终最多能有 dp(n, a_num, copy) 个 A
   int dp(int n, int a_num, int copy) {
       // base case
       if (n <= 0) {
           return a_num;
       }
       // 几种选择全试一遍，选择最大的结果
       return Math.max(
               Math.max(dp(n - 1, a_num + 1, copy),    // A
                       dp(n - 1, a_num + copy, copy)), // C-V
               dp(n - 2, a_num, a_num)        // C-A C-C
       );
   }

下面就继续走流程，用备忘录消除一下重叠子问题：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
HashMap<String, Integer> map = new HashMap();

   public int maxA(int N) {
       // 可以按 N 次按键，屏幕和剪切板里都还没有 A
       return dp(N, 0, 0);
   }

   // 对于 (n, a_num, copy) 这个状态，
   // 屏幕上能最终最多能有 dp(n, a_num, copy) 个 A
   int dp(int n, int a_num, int copy) {
       // base case
       if (n <= 0) {
           return a_num;
       }
       // 避免计算重叠子问题
       if (map.containsKey(n + "*" + a_num + copy)) {
           return map.get(n + "*" + a_num + copy);
       }
       // 几种选择全试一遍，选择最大的结果
       map.put(n + "*" + a_num + copy, Math.max(
               Math.max(dp(n - 1, a_num + 1, copy),    // A
                       dp(n - 1, a_num + copy, copy)), // C-V
               dp(n - 2, a_num, a_num)        // C-A C-C
       ));
       return map.get(n + "*" + a_num + copy);
   }

第二种思路

这种思路稍微有点复杂，但是效率高。继续走流程，「选择」还是那 4 个，但是这次只定义一个「状态」，也就是剩余的敲击次数 n。

这个算法基于这样一个事实，最优按键序列一定只有两种情况：

要么一直按 A：A,A,…A（当 N 比较小时）。

要么是这么一个形式：A,A,…C-A,C-C,C-V,C-V,…C-V（当 N 比较大时）。

因为字符数量少（N 比较小）时，C-A C-C C-V 这一套操作的代价相对比较高，可能不如一个个按 A；而当 N 比较大时，后期 C-V 的收获肯定很大。这种情况下整个操作序列大致是：开头连按几个 A，然后 C-A C-C 组合再接若干 C-V，然后再 C-A C-C 接着若干 C-V，循环下去。

换句话说，最后一次按键要么是 A 要么是 C-V。明确了这一点，可以通过这两种情况来设计算法：

1
2
3
4
5
6
7
8
int[] dp = new int[N + 1];
// 定义：dp[i] 表示 i 次操作后最多能显示多少个 A
for (int i = 0; i <= N; i++) {
    dp[i] = Math.max(
            这次按 A 键，
            这次按 C-V
        )
    }

对于「按 A 键」这种情况，就是状态 i - 1 的屏幕上新增了一个 A 而已，很容易得到结果：

1
2
// 按 A 键，就比上次多一个 A 而已
dp[i] = dp[i - 1] + 1;

但是，如果要按 C-V，还要考虑之前是在哪里 C-A C-C 的。

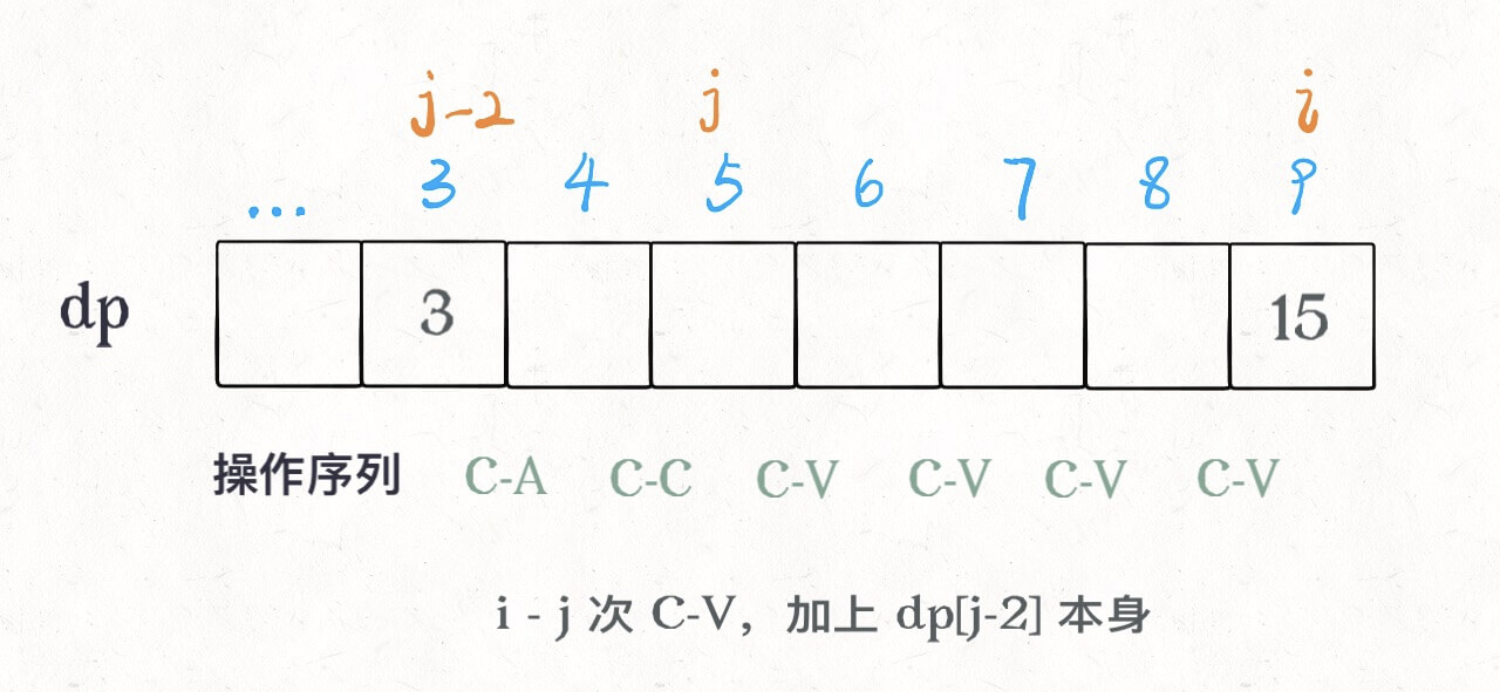
刚才说了，最优的操作序列一定是 C-A C-C 接着若干 C-V，所以用一个变量 j 作为若干 C-V 的起点。那么 j 之前的 2 个操作就应该是 C-A C-C 了：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public int maxA(int N) {
    int[] dp = new int[N + 1];
    dp[0] = 0;
    for (int i = 1; i <= N; i++) {
        // 按 A 键
        dp[i] = dp[i - 1] + 1;
        for (int j = 2; j < i; j++) {
            // 全选 & 复制 dp[j-2]，连续粘贴 i - j 次
            // 屏幕上共 dp[j - 2] * (i - j + 1) 个 A
            dp[i] = Math.max(dp[i], dp[j - 2] * (i - j + 1));
        }
    }
    // N 次按键之后最多有几个 A？
    return dp[N];
}

其中 j 变量减 2 是给 C-A C-C 留下操作数

坚持原创技术分享，您的支持将鼓励我继续创作！