发表于 | 分类于
字数统计: 462 | 阅读时长 ≈ 2分钟

198.打家劫舍

213.打家劫舍II

337.打家劫舍III

还是动态规划

假想你就是这个专业强盗，从左到右走过这一排房子，在每间房子前都有两种选择：抢或者不抢。

如果你抢了这间房子，那么你肯定不能抢相邻的下一间房子了，只能从下下间房子开始做选择。

如果你不抢这间房子，那么你可以走到下一间房子前，继续做选择。

当你走过了最后一间房子后，你就没得抢了，能抢到的钱显然是 0（base case）。

以上的逻辑很简单吧，其实已经明确了「状态」和「选择」：你面前房子的索引就是状态，抢和不抢就是选择。

「状态」：面前房子的索引

「选择」：抢或不抢

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
	//自顶向下
	public int dp(int[] nums, int start) {
		int res = Math.max(dp(nums, start + 1), nums[start] + dp(nums, start + 2));
		return res;
	}
	//自底向上
	public int rob(int[] nums) {
      int n = nums.length;
      int[] dp = new int[n + 2];
      for (int i = n - 1; i >= 0; i--) {
          dp[i] = Math.max(dp[i + 1], nums[i] + dp[i + 2]);
      }
      return dp[0];
  }
//当前状态转移只和dp[i]后两间相关 优化空间O(1)
  public int rob2(int[] nums) {
      int n = nums.length;
      int dp_i_1 = 0;
      int dp_i_2 = 0;
      int dp_i = 0;
      for (int i = n - 1; i >= 0; i--) {
          dp_i = Math.max(dp_i_1, nums[i] + dp_i_2);
          dp_i_2 = dp_i_1;
          dp_i_1 = dp_i;
      }
      return dp_i;
  }
  //二叉树题
  /**
   * [0]:不抢root
   * [1]:抢root
   */
  int[] dp(TreeNode root) {
      if (root == null) {
          return new int[]{0, 0};
      }
      int[] left = dp(root.left);
      int[] right = dp(root.right);
      //抢root 下家就不能抢
      int rob = root.val + left[0] + right[0];
      //不抢root 下家可以抢
      int not_rob = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);
      return new int[]{not_rob, rob};
  }

发表于 | 分类于
字数统计: 898 | 阅读时长 ≈ 4分钟

121.买卖股票的最佳时机

一、穷举框架

具体到每一天，看看总共有几种可能的「状态」，再找出每个「状态」对应的「选择」。我们要穷举所有「状态」，穷举的目的是根据对应的「选择」更新状态

1
2
3
4
for 状态1 in 状态1的所有取值：
    for 状态2 in 状态2的所有取值：
        for ...
            dp[状态1][状态2][...] = 择优(选择1，选择2...)

「选择」：买入、卖出、无操作
「状态」：天数、允许交易的最大次数、当前的持有状态(1持有，0未持有)

dp[3][2][1] ：今天是第三天，我现在手上持有着股票，至今最多进行 2 次交易

求dp[n - 1][K][0]

1
2
3
4
5
6
7
8
9
dp[i][k][0 or 1]
0 <= i <= n-1, 1 <= k <= K
n 为天数，大 K 为最多交易数
此问题共 n × K × 2 种状态，全部穷举就能搞定。

for 0 <= i < n:
    for 1 <= k <= K:
        for s in {0, 1}:
            dp[i][k][s] = max(buy, sell, rest)

二、状态转移框架

1
2
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
             	max(选择 rest,      选择 sell)

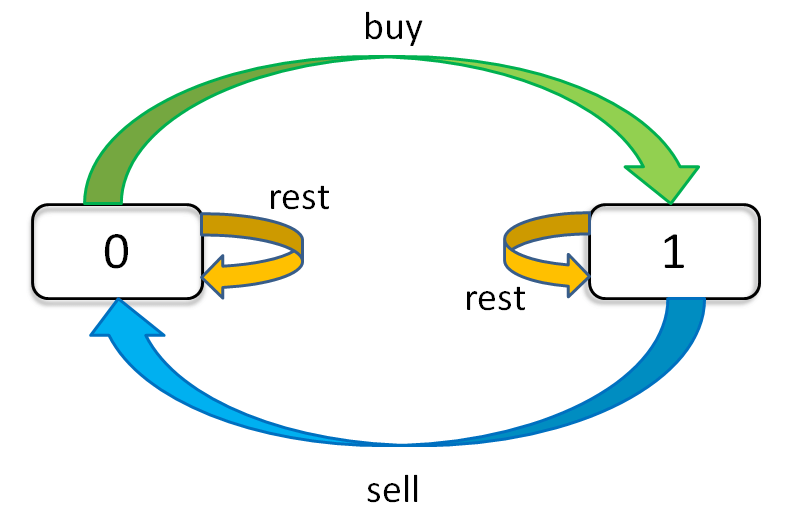
今天我没有持有股票，有两种可能：
要么是我昨天就没有持有，然后今天选择 rest，所以我今天还是没有持有；
要么是我昨天持有股票，但是今天我 sell 了，所以我今天没有持有股票了。

1
2
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])
              max(选择 rest,      选择 buy)

今天我持有着股票，有两种可能：
要么我昨天就持有着股票，然后今天选择 rest，所以我今天还持有着股票；
要么我昨天本没有持有，但今天我选择 buy，所以今天我就持有股票了。

1
dp[-1][k][0] = 0

因为 i 是从 0 开始的，所以 i = -1 意味着还没有开始，这时候的利润当然是 0 。

1
dp[-1][k][1] = -infinity

还没开始的时候，是不可能持有股票的，用负无穷表示这种不可能。

1
dp[i][0][0] = 0

因为 k 是从 1 开始的，所以 k = 0 意味着根本不允许交易，这时候利润当然是 0 。

1
dp[i][0][1] = -infinity

不允许交易的情况下，是不可能持有股票的，用负无穷表示这种不可能。

1
2
3
4
5
6
7
base case：
dp[-1][k][0] = dp[i][0][0] = 0
dp[-1][k][1] = dp[i][0][1] = -infinity

状态转移方程：
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])

⏬⏬⏬

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
public int maxProfit(int[] prices) {
       if (prices == null || prices.length == 0) {
           return 0;
       }
       int n = prices.length;
       int[][] dp = new int[n][2];
       for (int i = 0; i < n; i++) {
           if (i - 1 == -1) {
               dp[i][0] = 0;
               //   dp[i][0]
               // = max(dp[-1][0], dp[-1][1] + prices[i])
               // = max(0, -infinity + prices[i]) = 0
               dp[i][1] = -prices[i];
               //   dp[i][1]
               // = max(dp[-1][1], dp[-1][0] - prices[i])
               // = max(-infinity, 0 - prices[i])
               // = -prices[i]
               continue;
           }
           dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
           dp[i][1] = Math.max(dp[i - 1][1], -prices[i]);
       }
       return dp[n - 1][0];
   }

tips:

如果 buy，就要从利润中减去 prices[i]，如果 sell，就要给利润增加 prices[i]。今天的最大利润就是这两种可能选择中较大的那个。而且注意 k 的限制，我们在选择 buy 的时候，把 k 减小了 1，当然你也可以在 sell 的时候减 1，一样的。

发表于 | 分类于
字数统计: 453 | 阅读时长 ≈ 2分钟

76.最小覆盖子串

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
/* 滑动窗口算法框架 */
  void slidingWindow(String s, String t) {
      HashMap<Character, Integer> need, window;
      for (char c : t.toCharArray()) {
          need.put(c, need.getOrDefault(c, 0) + 1);
      }

      int left = 0, right = 0;
      int valid = 0;
      while (right < s.length()) {
          // c 是将移入窗口的字符
          char c = s.charAt(right);
          // 右移窗口
          right++;
          // 进行窗口内数据的一系列更新
      		...

          /*** debug 输出的位置 ***/
          System.out.printf("window: [%d, %d)\n", left, right);
          /********************/

          // 判断左侧窗口是否要收缩
          while (window needs shrink){
              // d 是将移出窗口的字符
              char d = s.charAt(left);
              // 左移窗口
              left++;
              // 进行窗口内数据的一系列更新
        		  ...
          }
      }

⏬⏬⏬

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
public String minWindow(String s, String t) {
       HashMap<Character, Integer> need = new HashMap<>();
       HashMap<Character, Integer> window = new HashMap<>();
       for (Character c : t.toCharArray()) {
           need.put(c, need.getOrDefault(c, 0) + 1);
       }
       int left = 0;
       int right = 0;
       //满足need条件的字符个数
       int vaild = 0;
       //记录最小覆盖子串的其实索引和长度
       int start = 0;
       int len = Integer.MAX_VALUE;
       while (right < s.length()) {
           //c是即将移入窗口的字符
           char c = s.charAt(right);
           //右移窗口
           right++;
           //进行窗口内数据更新
           if (need.containsKey(c)) {
               window.put(c, window.getOrDefault(c, 0) + 1);
               if (window.get(c).equals(need.get(c))) {
                   vaild++;
               }
           }
           //判断左侧窗口是否需要收缩
           while (vaild == need.size()) {
               //更新最小覆盖子串
               if (right - left < len) {
                   start = left;
                   len = right - left;
               }
               //d是即将移除的字符
               char d = s.charAt(left);
               //左移窗口
               left++;
               //进行窗口内数据更新
               if (need.containsKey(d)) {
                   if (window.get(d).equals(need.get(d))) {
                       vaild--;
                   }
                   window.put(d, window.get(d) - 1);
               }
           }
       }
       //返回最小覆盖子串
       return len == Integer.MAX_VALUE ? "" : s.substring(start, start + len);
   }

发表于 | 分类于
字数统计: 208 | 阅读时长 ≈ 1分钟 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int binarySearch(int[] nums, int target) {
    int left = 0, right = ...;

    while(...) {
        int mid = left + (right - left) / 2;
        if (nums[mid] == target) {
            ...
        } else if (nums[mid] < target) {
            left = ...
        } else if (nums[mid] > target) {
            right = ...
        }
    }
    return ...;
}

⏬⏬⏬

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int binarySearch(int[] nums, int target) {
    int left = 0; 
    int right = nums.length - 1; // 注意

    while(left <= right) {
        int mid = left + (right - left) / 2;
        if(nums[mid] == target)
            return mid; 
        else if (nums[mid] < target)
            left = mid + 1; // 注意
        else if (nums[mid] > target)
            right = mid - 1; // 注意
    }
    return -1;
}

tips:

分析二分查找的一个技巧是：不要出现 else，而是把所有情况用 else if 写清楚，这样可以清楚地展现所有细节。计算 mid 时需要防止溢出，代码中 left + (right - left) / 2 就和 (left + right) / 2 的结果相同，但是有效防止了 left 和 right 太大直接相加导致溢出。

发表于 | 分类于
字数统计: 388 | 阅读时长 ≈ 2分钟

111.二叉树的最小深度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
// 计算从起点 start 到终点 target 的最近距离
int BFS(Node start, Node target) {
    Queue<Node> q; // 核心数据结构
    Set<Node> visited; // 避免走回头路

    q.offer(start); // 将起点加入队列
    visited.add(start);
    int step = 0; // 记录扩散的步数

    while (q not empty) {
        int sz = q.size();
        /* 将当前队列中的所有节点向四周扩散 */
        for (int i = 0; i < sz; i++) {
            Node cur = q.poll();
            /* 划重点：这里判断是否到达终点 */
            if (cur is target)
                return step;
            /* 将 cur 的相邻节点加入队列 */
            for (Node x : cur.adj())
                if (x not in visited) {
                    q.offer(x);
                    visited.add(x);
                }
        }
        /* 划重点：更新步数在这里 */
        step++;
    }
}

tips:

BFS 的核心思想就是把一些问题抽象成图，从一个点开始，向四周开始扩散。问题的本质就是让你在一幅「图」中找到从起点 start 到终点 target 的最近距离。一般来说，我们写 BFS 算法都是用「队列」这种数据结构，每次将一个节点周围的所有节点加入队列。

BFS 相对 DFS 的最主要的区别是：BFS 找到的路径一定是最短的，但代价就是空间复杂度比 DFS 大很多

双向 BFS 优化，传统的 BFS 框架就是从起点开始向四周扩散，遇到终点时停止；而双向 BFS 则是从起点和终点同时开始扩散，当两边有交集的时候停止。

发表于 | 分类于
字数统计: 173 | 阅读时长 ≈ 1分钟 
1
2
3
4
5
6
7
8
9
10
result = []
void backtrack(路径, 选择列表):
    if 满足结束条件:
        result.add(路径)
        return

    for 选择 in 选择列表:
        做选择
        backtrack(路径, 选择列表)
        撤销选择

tips:

解决一个回溯问题，实际上就是一个决策树的遍历过程

需要思考 3 个问题：

1、路径：也就是已经做出的选择。

2、选择列表：也就是你当前可以做的选择。

3、结束条件：也就是到达决策树底层，无法再做选择的条件。

其核心就是 for 循环里面的递归，在递归调用之前「做选择」，在递归调用之后「撤销选择」

发表于 | 分类于
字数统计: 264 | 阅读时长 ≈ 1分钟

今天刷minimum-window-substring问题时，写的代码跑通了267/268的测试用例，最后一个没跑通，最后发现是

window.get(d) == need.get(d)出的问题，两个值都是371但是结果是false，然后才想起来Interger底部是有缓存的，关系如下：

Integer与int类型的关系，可以简单的回答，Integer是int的包装类，int的默认值是0，而Integer的默认值是null（jdk1.5的新特性 自动装箱和拆箱，Integer.valueOf（） 和xx.intValue（） ）,需要注意的是Integer里面默认的缓存数字是-128-127。

1、Integer与Integer相互比较，数据在-128-127范围内，就会从缓存中拿去数据，比较就相等；如果不在这个范围，就会直接新创建一个Integer对象，使用 == 判断的是两个内存的应用地址，所以自然不相等，应该用equals来判断值是否想等

2、Integer和int类型相比，在jdk1.5,会自动拆箱，然后比较栈内存中的数据，所以没有不想等的情况

发表于 | 分类于
字数统计: 106 | 阅读时长 ≈ 1分钟 
1
2
3
4
5
6
7
# 初始化 base case
dp[0][0][...] = base
# 进行状态转移
for 状态1 in 状态1的所有取值：
    for 状态2 in 状态2的所有取值：
        for ...
            dp[状态1][状态2][...] = 求最值(选择1，选择2...)

tips:

明确 base case -> 明确「状态」-> 明确「选择」 -> 定义 dp 数组/函数的含义

通过「备忘录」或者「dp table」的方法来优化递归树

发表于 | 分类于
字数统计: 450 | 阅读时长 ≈ 2分钟

最近换了新电脑，重新整环境的时候图快，下载node的时候下载的是最新版：node当前版14.0.0。然后安装hexo，从github拉取hexo博客项目，然后跑npm install，都没啥问题。但是在项目下面执行任何hexo的命令的时候，就会出现一个错误：

1
2
3
4
5
6
7
8
9
10
11
12
13
(node:62227) Warning: Accessing non-existent property 'lineno' of module exports inside circular dependency
(Use `node --trace-warnings ...` to show where the warning was created)
(node:62227) Warning: Accessing non-existent property 'column' of module exports inside circular dependency
(node:62227) Warning: Accessing non-existent property 'filename' of module exports inside circular dependency
(node:62227) Warning: Accessing non-existent property 'lineno' of module exports inside circular dependency
(node:62227) Warning: Accessing non-existent property 'column' of module exports inside circular dependency
(node:62227) Warning: Accessing non-existent property 'filename' of module exports inside circular dependency
(node:62227) Warning: Accessing non-existent property 'lineno' of module exports inside circular dependency
(node:62227) Warning: Accessing non-existent property 'column' of module exports inside circular dependency
(node:62227) Warning: Accessing non-existent property 'filename' of module exports inside circular dependency
(node:62227) Warning: Accessing non-existent property 'lineno' of module exports inside circular dependency
(node:62227) Warning: Accessing non-existent property 'column' of module exports inside circular dependency
(node:62227) Warning: Accessing non-existent property 'filename' of module exports inside circular dependency

继续跑hexo s、hexo clean、hexo g都是可以的，也没报错。

当我跑hexo s的时候是可以正常预览的。

但是当我跑hexo g的时候，命令可以跑而且没报错，但是生成的文件是0kb的，/public/index.html里面没有任何内容。

找了好久原因，发现是node版本的问题。

下n来管理node的版本。

1
$ sudo npm i -g n

然后将node替换为稳定版：

1
$ sudo n stable

然后查看node的版本：

1
2
$ node -v
v12.18.3

先清理，然后再生成：

1
2
$ hexo clean
$ hexo g

然后产看生成的public文件夹中index.html的大小，是有内容的。正常生成了 -。-